突然ですが、かけ算の問題です。
例）
４台の三輪車のぜんぶのタイヤの数は？
式は、「４×３」？
それとも、「３×４」？
さて、あなたはお子さんから尋ねられた時、答えられますか？
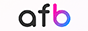
ドラゼミは進度が早い
ドラゼミでは、かけ算は9月号から始まります。
そして11月号の前半で終わり、11月号の後半は、分数です。
長女の小学校では、分数は3学期に習うので、学校の勉強よりかなり進んでいます。
式で困った
9月号で習うのは、2の段と5の段。
文章問題もひっかけが無く、すんなりクリアした長女。
しかし、異変は10月号で起こった。
↑まとめの問題で、このとおり。
単純に数字が出てきた順番に「9×6」と書いた模様。
完全にひっかかっている。
答えは「6×9」。
そして、発展問題では、全問間違い…
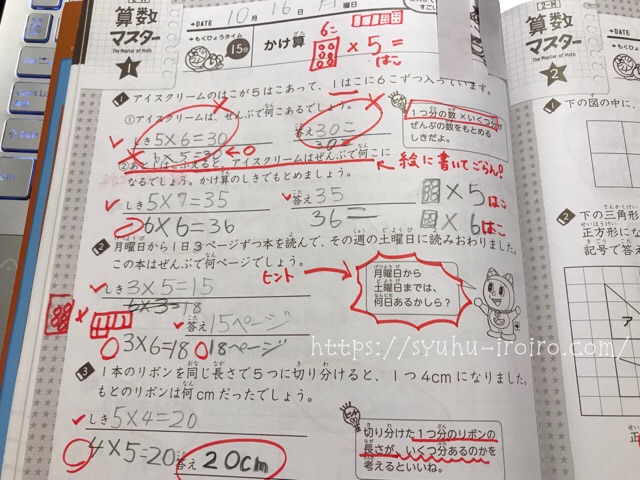
ヒントが書いてあるのに、全く読まないのが長女…。
ヒントを強調したらなんとか解けたけど、どうも、文章問題の内容を「1つ分の数×いくつ分」に当てはめることが苦手なようだ。
解答書には、「三年生で習う割り算で困らないように、かけ算の式の決まりをしっかり身につけましょう」とある。
ひえっ！
少し焦った私は、長女が暇そうな時に、口頭でかけ算の文章問題を出して（遊びで使うような道具を使った親しみやすい問題など）意識的にかけ算の式を作ることに慣れさせてみた。
最初は嫌がっていた長女も、数をこなすと、何となくコツを掴み、確信をもって正解するようになってきた。
そして、11月号。
…解けたーーーー！！！
「1つ分の数×いくつ分」を判別するイメージが、正確に身についたようで良かった。
ドラさんが大事なこと言ってた
今回の「かけ算の式、苦戦事件」をふまえ、9月号から11月号までのテキストを読み直していた私、すごいことに気が付いた。
11月号、6の段の説明部分。
ドラえもんのセリフに注目。
「1つ分の数と答えの単位は、同じになるよ」！？
…えっっ？
「1つ分の数×いくつ分」で覚えるより、単純明快で分かりやすっ！！！
これを知っていたか長女に確認すると、「見てなかった～」ですと。
そして、「これだと見直ししやすいね」と言ったけど、あなた、全く見直ししない主義じゃないですか…（怒）
そんなわけで、後付けで知った、「1つ分の数と答えの単位は同じ」も、かけ算の式を作る際のポイントです！
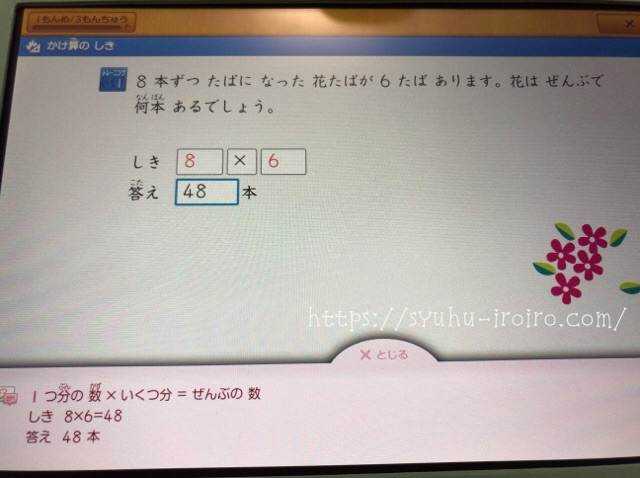
↑ちなみに、スマイルゼミでも、このような解説です。
冒頭の問題の答え
さて、もう一度冒頭の問題を挙げます。
（問題）４台の三輪車のぜんぶのタイヤの数は？
…もう答えられますね♪
3「輪」×4「台」＝12「輪」（1つ分の数と答えの単位は同じ）なので、式は「3×4」。
学校より一歩踏み込んだ学習
ドラゼミ11月号より。
教科書をザっと見てきたら、0の段は習わないような感じ。
ドラゼミでは、0の段も習う。
「かえるのおへその数」という例えが上手い！！
いくら掛けても、そりゃ0だわな…
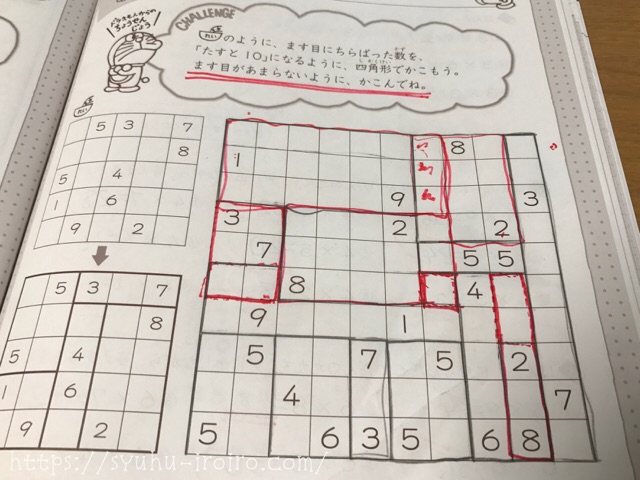
↑こんな数字を使った図形パズルも。
国語の読解問題も、かなり難易度が上がってきた感じがする。
比較的国語が得意（だった）な長女も、最近はミスが多くなってきた。
これは書き直した後なので正解したものですが、丸つけは訂正しまくりで、真っ赤です。
まとめ
- かけ算の式は、「1つ分の数×いくつ分」と「1つ分の数と答えの単位は同じ」を覚える！
- ドラゼミのテキストには重要なヒントが書いてあるので、親も見逃せない…
-
-
九九が覚えられない！スマイルゼミなら苦痛じゃなくなる、その秘密。
小2算数の山場は、何と言っても2学期の九九です！ 九九の暗唱が毎日の宿題になります。 12月中に全ての段が終わるよう先生も必死です。 私は昔、がむしゃらに覚えようとしたので、苦痛でしかなかった。 （ ...
Copyright secured by Digiprove © 2017